5. Mass and Center of Mass
Exercises
-
A \(6\) cm rod has linear density given by \(\delta(x)=(2x+1)\,\dfrac{\text{gm}}{\text{cm}}\) where \(x\) is measured from one end.

\(M=42\) gm
The mass is \[\begin{aligned} M&=\int_0^6 \delta(x)\,dx=\int_0^6 (2x+1)\,dx \\ &=\left[\dfrac{}{}x^2+x\right]_0^6=36+6=42 \,\text{gm} \end{aligned}\]
-
A \(4\) cm rod has linear density given by \(\delta(x)=(5x^3-3x+2)\,\dfrac{\text{gm}}{\text{cm}}\) where \(x\) is measured from one end.

\(M=304\,\text{gm}\)
The mass is \[\begin{aligned} M&=\int_0^4 \delta(x)\,dx=\int_0^4 (5x^3-3x+2)\,dx \\ &=\left[\dfrac{5x^4}{4}-\dfrac{3x^2}{2}+2x\right]_0^4 =320-24+8=304\,\text{gm} \end{aligned}\]
-
A chocolate bar which is \(6\) in long has linear density given by \(\delta(x)=\ln(x+2)\,\dfrac{\text{oz}}{\text{in}}\) where \(x\) is measured from one end.

Recall: \(\displaystyle \int \ln u\,du=u\ln u-u+C\).
\(M=(22\ln 2-6)\,\text{oz}\approx 9.25\,\text{oz}\)
The mass is \[ M=\int_0^6 \ln(x+2)\,dx \] To use the formula \(\displaystyle \int \ln u\,du=u\ln u-u+C\), we make the change of variables \(u=x+2\) and \(du=dx\). For the limits, \(x=0\) when \(u=2\) and \(x=6\) when \(u=8\). So \[\begin{aligned} M&=\int_2^8 \ln u\,du=\left[\dfrac{}{}u\ln u-u\right]_2^8 \\ &=(8\ln8-8)-(2\ln2-2) \\ &=(8\cdot3\ln2-8)-(2\ln2-2) \\ &=(22\ln2-6)\,\text{oz} \approx 9.25\,\text{oz} \end{aligned}\]
-
A bar which is \(5\) in long has linear density given by \(\delta(x)=xe^x\) \(\dfrac{\text{oz}}{\text{in}}\) where \(x\) is measured from one end.

Use integration by parts.
\(M=(4e^5+1)\,\text{oz}\approx 595.\,\text{oz}\)
The mass is \[ M=\int_0^5 \delta(x)\,dx=\int_0^5 xe^x\,dx \] We use integration by parts with \[\begin{array}{ll} u=x & dv=e^x\,dx \\ du=dx \quad & v=e^x \end{array}\] So \[\begin{aligned} M&=\left[xe^x-\int e^x\,dx\right]_0^5 =\left[\dfrac{}{}xe^x-e^x\right]_0^5 \\ &=(4e^5+1)\,\text{oz} \approx 595.\,\text{oz} \end{aligned}\]
-
A \(6\) cm rod has linear density given by \(\delta(x)=\left(\dfrac{1}{8}+\dfrac{2}{(x+4)^2}\right) \,\dfrac{\text{gm}}{\text{cm}}\) where \(x\) is measured from one end.
^2.jpg)
\(M=\dfrac{21}{20}\,\text{gm}\)
The mass is \[ M=\int_0^6 \delta(x)\,dx=\int_0^6\left(\dfrac{1}{8}+\dfrac{2}{(x+4)^2}\right)\,dx \] Using substitution with \(u=x+4\) and \(du=dx\). For the limits, \(x=0\) when \(u=4\) and \(x=6\) when \(u=10\). So \[ \begin{aligned} M&=\int_4^{10}\left(\dfrac{1}{8}+\dfrac{2}{u^2}\right)\,du =\left[\dfrac{1}{8}u-\dfrac{2}{u}\right]_4^{10}\\ &=\left(\dfrac{1}{8}10-\dfrac{2}{10}\right)-\left(\dfrac{1}{8}4-\dfrac{2}{4}\right)\\ &=\dfrac{5}{4}-\dfrac{1}{5}-\dfrac{1}{2}+\dfrac{1}{2}\\ &=\dfrac{25}{20}-\dfrac{4}{20}=\dfrac{21}{20}\,\text{gm} \end{aligned} \]
-
Find the total mass and the center of mass for four discrete masses lying on the \(x\)-axis where the masses and positions indicated below are in grams and centimeters. \[\begin{aligned} m_1&=7 &m_2&=5 &m_3&=2 &m_4&=6 \\ x_1&=-3 &x_2&=-2 &x_3&=4 &x_4&=7 \end{aligned}\]
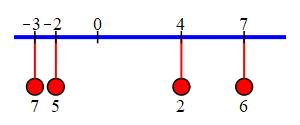
\(M=20\) gm
\(\bar{x}=\dfrac{19}{20}\,\text{cm}=.95\,\text{cm}\)The total mass is: \[\begin{aligned} M&=m_1+m_2+m_3+m_4 \\ &=7+5+2+6=20\,\text{gm} \end{aligned}\] The first moment is: \[\begin{aligned} M_1&=m_1x_1+m_2x_2+m_3x_3+m_4x_4 \\ &=7(-3)+5(-2)+2(4)+6(7)=19\,\text{gm-cm} \end{aligned}\]
So the center of mass is at: \[ \bar{x}=\dfrac{M_1}{M}=\dfrac{19}{20}\,\text{cm} =.95\,\text{cm} \] The plot shows the location of the center of mass.
-
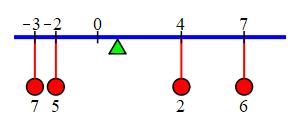
A \(6\) cm rod has linear density \(\delta(x)=(2x+1)\,\dfrac{\text{gm}}{\text{cm}}\) where \(x\) is measured from one end. The mass was found in previous exercise.

\(\bar{x}=\dfrac{27}{7}\,\text{cm}\approx3.86\,\text{cm}\)
From a previous exercise we know the mass is \[ M=42 \] The first moment is \[\begin{aligned} M_1&=\int_0^6 x\delta(x)\,dx=\int_0^6 x(2x+1)\,dx \\ &=\left[\dfrac{2x^3}{3}+\dfrac{x^2}{2}\right]_0^6 =144+18=162\,\text{gm-cm} \end{aligned}\]
So the center of mass is at: \[ \bar{x}=\dfrac{M_1}{M}=\dfrac{162}{42}=\dfrac{27}{7}\,\text{cm} \approx3.86\,\text{cm} \] The plot shows the location of the center of mass.
The density \(\delta(x)=(2x+1)\) is bigger on the right and \(\bar{x}=\dfrac{27}{7}\,\text{cm}\approx3.86\,\text{cm}\) is inside the bar but right of the middle.
-
Find the center of mass of a \(4\) cm rod has linear density \(\delta(x)=(5x^3-3x+2)\,\dfrac{\text{gm}}{\text{cm}}\) where \(x\) is measured from one end. The mass was found in previous exercise.

\(\bar{x}=\dfrac{61}{3}\approx 3.21\) gm
From a previous exercise we know the mass is \[ M=304 \] The first moment is \[\begin{aligned} M_1&=\int_0^4 x\delta(x)\,dx=\int_0^4 x(5x^3-3x+2)\,dx \\ &=\left[\dfrac{}{}x^5-x^3+x^2\right]_0^4 \\ &=1024-64+16=976\,\text{gm-cm} \end{aligned}\]
So the center of mass is at: \[ \bar{x}=\dfrac{M_1}{M}=\dfrac{976}{304}=\dfrac{61}{19}\approx 3.21\,\text{cm} \] The plot shows the location of the center of mass.

-
Find the mass and the center of mass of a \(30\) cm rod that has linear density \(\delta(x)=\dfrac{1}{2}x^2\) \(\dfrac{\text{gm}}{\text{cm}}\) where \(x\) is measured from one end.

\(M=4500\) gm
\(\bar{x}=\dfrac{45}{2}\,\text{cm}=22.5\,\text{cm}\)The mass is: \[\begin{aligned} M&=\int_0^{30} \delta(x)\,dx=\int_0^{30} \dfrac{1}{2}x^2\,dx \\ &=\left[\dfrac{1}{6}x^3\right]_0^{30} =\dfrac{30^3}{6} =4500 \,\text{gm} \end{aligned}\] The first moment is: \[\begin{aligned} M_1&=\int_0^{30} x\delta(x)\,dx=\int_0^{30} x\dfrac{1}{2}x^2\,dx \\ &=\left[\dfrac{1}{8}x^4\right]_0^{30} =\dfrac{30^4}{8} = 101250\,\text{gm} \end{aligned}\]
So the center of mass is at: \[\begin{aligned} \bar{x}&=\dfrac{M_1}{M}=\dfrac{30^4}{8}\dfrac{6}{30^3} \\ &=\dfrac{45}{2}\,\text{cm} =22.5\,\text{cm} \end{aligned}\] The plot shows the location of the center of mass.

-
Find the moment of inertia for four discrete masses lying on the \(x\)-axis and rotating about \(x_0=0\), where the masses and positions indicated below are in grams and centimeters. \[\begin{aligned} m_1&=7 &m_2&=5 &m_3&=2 &m_4&=6 \\ x_1&=-3 &x_2&=-2 &x_3&=4 &x_4&=7 \end{aligned}\]
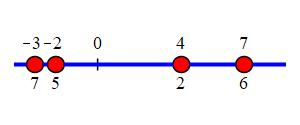
\(I=409\) gm-cm\(^2\)
Since \(x_0=0\), the moment of intertia is just the second moment. \[\begin{aligned} I&=M_2=m_1x_1^2+m_2x_2^2+m_3x_3^2+m_4x_4^2 \\ &=7(-3)^2+5(-2)^2+2(4)^2+6(7)^2=409\,\text{gm-cm}^2 \end{aligned}\]
-
Find the mass, center of mass and moment of inertia of a \(6\) m bar on the \(x\)-axis between \(x=0\) and \(x=6\) rotating about \(x_0=4\),
-
with uniform density \(\delta=3\) \(\dfrac{\text{kg}}{\text{m}}\).
\(M=18\,\text{kg}\)
\(\bar{x}=3\,\text{m}\)
\(I=72\,\text{kg-m}^2\)The mass is: \[\begin{aligned} M&=\int_0^6 \delta(x)\,dx=\int_0^6 3\,dx \\ &=\left[\dfrac{}{}3x\right]_0^6=18\,\text{kg} \end{aligned}\] The first moment is: \[\begin{aligned} M_1&=\int_0^6 x\delta(x)\,dx=\int_0^6 3x\,dx \\ &=\left[3\dfrac{x^2}{2}\right]_0^6=54\,\text{kg-m} \end{aligned}\] The second moment is: \[\begin{aligned} M_2&=\int_0^6 x^2\delta(x)\,dx=\int_0^6 3x^2\,dx \\ &=\left[\dfrac{}{}x^3\right]_0^6=216\,\text{kg-m}^2 \end{aligned}\] So the center of mass is at: \[ \bar{x}=\dfrac{M_1}{M}=\dfrac{54}{18}=3\,\text{m} \] Since \(x_0=4\), the moment of intertia is: \[\begin{aligned} I&=M_2-2x_0M_1+x_0^2M \\ &=216-8\cdot54+16\cdot18=72\,\text{kg-m}^2 \end{aligned}\]
Since the density is uniform, the mass, \(M=18\), is just the length times the density.
Since the density is uniform, the center of mass, \(\bar{x}=3\), is at the geomertrical center of the bar which is also called the centroid. -
with linear density \(\delta(x)=x\) \(\dfrac{\text{kg}}{\text{m}}\).
\(M=18\,\text{kg}\)
\(\bar{x}=4\,\text{m}\)
\(I=36\,\text{kg-m}^2\)The mass is: \[\begin{aligned} M&=\int_0^6 \delta(x)\,dx=\int_0^6 x\,dx \\ &=\left[\dfrac{x^2}{2}\right]_0^6=18\,\text{kg} \end{aligned}\] The first moment is: \[\begin{aligned} M_1&=\int_0^6 x\delta(x)\,dx=\int_0^6 x^2\,dx \\ &=\left[\dfrac{x^3}{3}\right]_0^6=72\,\text{kg-m} \end{aligned}\] The second moment is: \[\begin{aligned} M_2&=\int_0^6 x^2\delta(x)\,dx=\int_0^6 x^3\,dx \\ &=\left[\dfrac{x^4}{4}\right]_0^6=324\,\text{kg-m}^2 \end{aligned}\] So the center of mass is at: \[ \bar{x}=\dfrac{M_1}{M}=\dfrac{72}{18}=4\,\text{m} \] Since \(x_0=4\), the moment of intertia is: \[\begin{aligned} I&=M_2-2x_0M_1+x_0^2M \\ &=324-8\cdot72+16\cdot18=36\,\text{kg-m}^2 \end{aligned}\]
Notice that the mass of both bars is \(M=18\). Since the lengths are both \(L=6\), the average densities are the same: \[ \delta_\text{ave}=\dfrac{M}{L}=\dfrac{18}{6}=3 \] Since the non-uniform bar is heavier for \(x>3\), the center of mass, \(\bar{x}=4\), is on that side.
-
-
If we measure \(x\) from one end of the bar, find the net charge on a \(6\) m bar whose linear charge density is:
(In each case, explain why the answer is reasonable by explaining where there is positive or negative charge.)-
\(\delta_e(x)=3-2x\) \(\dfrac{\text{coul}}{\text{m}}\)

\(Q=-18\) coul
The net charge is: \[\begin{aligned} Q&=\int_0^6 \delta_e(x)\,dx=\int_0^6 3-2x\,dx \\ &=\left[\dfrac{}{}3x-x^2\right]_0^6 =18-36=-18\,\text{coul} \end{aligned}\] There is the positive charge for \(0 \le x \lt \dfrac{3}{2}\) but negative charge for \(\dfrac{3}{2} \lt x \le 6\). So there is more negative charge.
-
\(\delta_e(x)=x-3\) \(\dfrac{\text{coul}}{\text{m}}\)

\(Q=0\) coul
The net charge is: \[\begin{aligned} Q&=\int_0^6 \delta_e(x)\,dx=\int_0^6 x-3\,dx \\ &=\left[\dfrac{x^2}{2}-3x\right]_0^6 =18-18=0\,\text{coul} \end{aligned}\] There is the positive charge on half the bar and negative charge on the other half.
-
\(\delta_e(x)=x-2\) \(\dfrac{\text{coul}}{\text{m}}\)

\(Q=6\) coul
The net charge is: \[\begin{aligned} Q&=\int_0^6 \delta_e(x)\,dx=\int_0^6 x-2\,dx \\ &=\left[\dfrac{x^2}{2}-2x\right]_0^6 =18-12=6\,\text{coul} \end{aligned}\] There is the negative charge for \(0 \le x \lt 2\) but positive charge for \(2 \lt x \le 6\). So there is more positive charge.
-
-
Find the total weight of a \(12\) ft rod with linear density \(\delta(x)=x\sqrt{x^2+1}\) \(\dfrac{\text{lb}}{\text{ft}}\) if \(x\) is measured from one end.
\(M=\dfrac{1}{3}(145^{3/2}-1)\,\text{lb} \approx581.7\,\text{lb}\)
The mass is \[ M=\int_0^{12} \delta(x)\,dx=\int_0^{12} x\sqrt{x^2+1}\,dx \] We make the substitution \(u=x^2+1\) and \(du=2x\,dx\): \[\begin{aligned} M&=\dfrac{1}{2}\int_1^{145} \sqrt{u}\,du =\dfrac{1}{2}\left[\dfrac{2u^{3/2}}{3}\right]_1^{145} \\ &=\dfrac{1}{3}(145^{3/2}-1)\,\text{lb} \approx581.7\,\text{lb} \end{aligned}\]
-
Find the total mass and the center of mass for a \(10\) m rod if the linear density is \(\delta(x)=e^x\) \(\dfrac{\text{kg}}{\text{m}}\) where \(x\) is measured from one end.
\(M=(e^{10}-1)\,\text{kg}\)
\(\bar{x}=\dfrac{9e^{10}+1}{e^{10}-1}\,\text{m} \approx9\,\text{m}\)The mass is: \[ M=\int_0^{10} \delta(x)\,dx=\int_0^{10} e^x\,dx =\left[\dfrac{}{}e^x\right]_0^{10}=(e^{10}-1)\,\text{kg} \] The first moment is: \[ M_1=\int_0^{10} x\delta(x)\,dx=\int_0^{10} xe^x\,dx \] To compute this integral, we use the parts: \[\begin{array}{ll} u=x & dv=e^x\,dx \\ du=dx \quad & v=e^x \end{array}\] So: \[\begin{aligned} M_1&=xe^x-\int e^x\,dx \\ &=\left[\dfrac{}{}xe^x-e^x\right]_0^{10}=(9e^{10}+1)\,\text{kg-m} \end{aligned}\] So the center of mass is: \[ \bar{x}=\dfrac{M_1}{M} =\dfrac{9e^{10}+1}{e^{10}-1}\,\text{m} \approx9\,\text{m} \]
-
Find the moment of inertia of a \(2\) in bar with linear density \(\delta(x)=\sqrt{x^3+1}\) \(\dfrac{\text{oz}}{\text{in}}\) if \(x\) is measured from one end and the rod rotates about that end.
\(I=\dfrac{52}{9}\,\text{oz-in}^2\)
Since \(x_0=0\), the moment of intertia is just the second moment. \[ I=M_2=\int_0^2 x^2\delta(x)\,dx=\int_0^2 x^2\sqrt{x^3+1}\,dx \] We make the substitution \(u=x^3+1\) and \(du=3x^2\,dx\): \[\begin{aligned} I&=\dfrac{1}{3}\int_1^9 \sqrt{u}\,du =\dfrac{1}{3}\left[\dfrac{2u^{3/2}}{3}\right]_1^9 \\ &=\dfrac{2}{9}(9^{3/2}-1) =\dfrac{52}{9}\,\text{oz-in}^2 \end{aligned}\]
-
Find the net charge on a rod with length \(3\pi\) cm and linear charge density \(\delta_e=\sin x\) \(\dfrac{\text{coul}}{\text{cm}}\) if \(x\) is measured from one end.

\(Q=2\) coul
The net charge is \[\begin{aligned} Q&=\int_0^{3\pi} \delta_e(x)\,dx=\int_0^{3\pi} \sin x\,dx =\left[\dfrac{}{}-\cos x\right]_0^{3\pi} \\ &=-\cos(3\pi)--\cos(0)=2\,\text{coul} \end{aligned}\]
In each problem, find the total mass.
In each problem, find the center of mass.
Review Exercises
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum